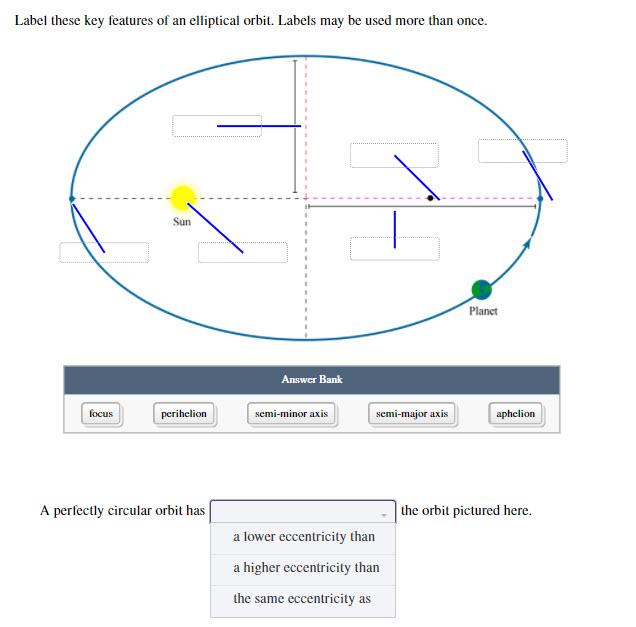
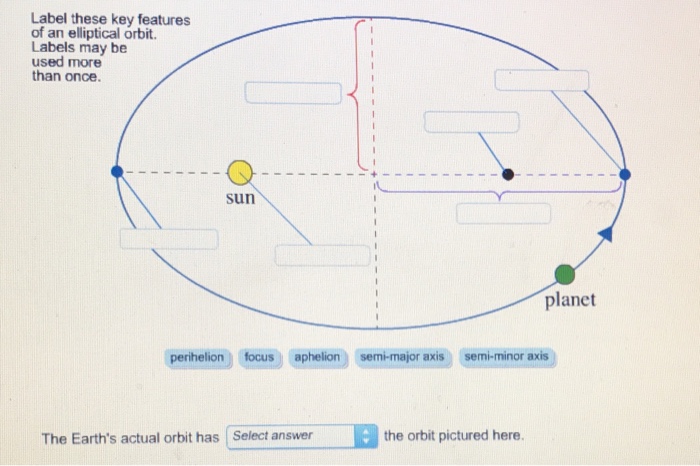
Label These Key Features of an Elliptical Orbit

IB1 The Elliptical Orbit. Such extremely elongated orbits have the advantage of long dwell times at a point in the sky during the approach to.

Hw 8 Kepler S Laws Flashcards Quizlet

This expression allows us to give a simple geometric interpretation of the eccentric anomaly Consider Figure 45Let represent the elliptical orbit of a planet about the Sun Let be the major axis of the orbit where is the perihelion point the aphelion point and the geometric center.

. This low value makes the elliptic orbit of earth almost a perfect circle. All of the planets in the Solar System have elliptical orbits though their eccentricity varies. The shorter line is the minor axis.

The higher the value of eccentricity the flatter and more elongated the shape of the elliptic orbit will be. Likewise half of the minor axis is the semi-minor axis. A A Foucault pendulum shows predictable changes in its direction of swing.

The range for eccentricity is 0 e 1 for an ellipse. One of the key features of an elliptical orbit is that the satellite in this type of orbit moves much faster when it is close to the earth than when it is farther away. IB1 The Elliptical Orbit.

Show transcribed image text Label these key features of an elliptical orbit Labels may be used more than once. Label these key features of an elliptical orbit. Label these key features of an elliptical orbit Labels may be used more than once.

The eccentricity of the Earths elliptical orbit is at present measured to be 00167. The fraction of a complete orbit is. Label this as Ellipse 1.

One of the key features of an elliptical orbit is that the satellite in this type of. Objects in elliptical trajectories follow predictable paths and this allows us to constrain the problem mathematically. We know the orbital parameters of a planets motion around the Sun.

This includes the special case of a circular orbit with eccentricity equal to 0In a stricter sense it is a Kepler orbit with the eccentricity greater than 0 and less than 1 thus excluding the circular orbit. Which has the greater effect on tides during a single month. In fact to describe an elliptical orbit in space we only need.

Planets move fastest at the perihelion. In astrodynamics or celestial mechanics an elliptic orbit or elliptical orbit is a Kepler orbit with an eccentricity of less than 1. Consequently the total energy ξ is negative.

Where will the planet be in its orbit at some later time t. B The apparent diameter of the Sun shows predictable changes. The total energy of a planet in an elliptical orbit depends only on the length a of the semimajor axis not on the length of the minor axis.

The range for eccentricity is 0 e 1 for an ellipse. The circle is a special case with e 0. Labels may be used more than once.

Consequently the total energy ξ is negative. The time to go around an elliptical orbit once depends only on the length a of the semimajor axis not on the length of the minor axis. 5The diagram below represents the elliptical orbit of a moon revolving around a planet.

Learn for free about math art computer programming economics physics chemistry biology medicine finance history and more. Half of the major axis is the semi-major axis. Using a clean sheet of paper and the same string as above draw another ellipse with the foci thumb tacks farther.

The circle is a special case with e 0. At any point in its orbit a planets total distance from these 2 focus points stays the same. A planets semi-major axis is related to its orbital period planets with smaller orbits take less time to complete one orbit label these key features of an elliptical orbit.

Note these on the data table. Note this on the data table. The sun is located at one focus of a planets orbit.

In what year will all cycles affecting the tides coincide again to cause maximum high and low tides. A Highly Elliptical Orbit HEO is a highly eccentrical orbit with a low perigee altitude of under 1000 km and a high apogee altitude of over 35756 km. This means that the bottom of the fraction in the orbit equation Eq.

Semimajor axis a is positive for an elliptical orbit. It follows that and see Section A9 where is the orbital major radius and the eccentricity. An elliptical orbit occurs when a circular orbit is disrupted by forces such as the gravity of nearby objects and follows a relatively stable but not circular path.

Semimajor axis a is positive for an elliptical orbit. The eccentricity of an elliptical orbit is defined by the ratio e ca where c is the distance from the center of the ellipse to either focus. Calculate the eccentricity of your ellipse.

If the orbit is circular then this is easy. An ellipse also has 2 lines of symmetry. The longer line is the major axis.

A lower eccentricity than a. An elliptical orbit can have an eccentricity up to 1. Labels may be used more than once.

1 Sun Planet Answer Bank focus perihelion semi-minor axis semi-major axis aphelion A perfectly circular orbit has the orbit pictured here. For objects orbiting the sun we have a major constraint-we know the orbit is elliptical and we know the main gravitational force acting on the body is the sun. T 2 4 π 2 a 3 G M.

The foci of this orbit are the points labeled F1 and F2. What is the approximate eccentricity of this elliptical orbit. Examine a globe or map of the earth.

E t o t G M m 2 a. The elliptical orbit of the earth around the sun or the elliptical orbit of the moon around the earth. Once it reaches the value of 1 it becomes parabolic and no longer elliptical.

Planets move in elliptical orbits. Planets sweep out equal areas in equal times. The Highly Elliptical term refers to the shape of the ellipse and the eccentricity of the orbit.

A planets semi-major axis is related to its orbital period. However the magnitude of the product e cosnu is never greater than one. Period P semimajor axis a eccentricity eWe also know the time T when the planet reaches its perihelion passage.

Sun planet perihelion focus aphelion semi-major axis semi-minor axis The Earths actual orbit has Select answer the orbit pictured here. Elliptical Orbits 0 e 1 If the eccentricity is between 0 and 1 then the radius of the orbit varies with the true anomaly. Keplers equation for motion around an orbit The problem is this.

The eccentricity of an elliptical orbit is defined by the ratio e ca where c is the distance from the center of the ellipse to either focus. Khan Academy is a nonprofit with the mission of providing a free world-class education for anyone anywhere. In a wider sense it is a Keplers orbit with.

Solved Label These Key Features Of An Elliptical Orbit Chegg Com

Solved Label These Key Features Of An Elliptical Orbit Chegg Com

Solved Label These Key Features Of An Elliptical Orbit Chegg Com

Solved Label These Key Features Of An Elliptical Orbit Chegg Com